TensorFlow2（４）２分類ニューラルネットのsource codeを読んでみる

太平洋高気圧が北へ押しやった梅雨前線がちょうど日本列島の上にある今日も雨降り．屋外を通って木材を搬入すると濡れてしまうのでシャワールーム作りはお休みです．

てなわけで、雨降りでもやれるのはTensorFlowだけであります．

「TensorFlow2プログラミング実装ハンドブック」第４章のsource codeを見てゆきます．

でも、クラスの中で何やってるのかがさっぱりわからん......

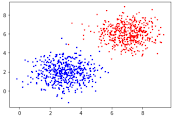
第４章前半で実装するのはこのニューラルネットです．xを２つの山に分類します．

In[1]: ２次元Ｘベクトルを1000個作る

ニューラルネットに投入するものです．

これだけで500個のベクトルを作れるのは便利でいいや．

   x1 = np.random.randn(500,2) + np.array([3, 2])
教師データも作っています．

   t1 = np.array([[0] for i in range(500)])

分布が２つの雲状になっているので、赤と青に分類するのがニューラル君にさせたい仕事です．

In[3]: 上の図のニューラルネットを定義する

MLPはmulti layer perseptronの略かな？

class MLP(tf.keras.Model):          Kerasから継承

    def __init__(self, hidden_dim, output_dim):        隠れ層２次元、出力層１次元として後で呼び出されることになる

        self.l1 = tf.keras.layers.Dense(hidden_dim, activation='sigmoid')  隠れ層L1

        self.l2 = tf.keras.layers.Dense(output_dim, activation='sigmoid')  出力層L2

    def call(self, x):     ニューラルネット本体

        h = self.l1(x)   隠れ層L1の計算

        y = self.l2(h)   出力層L2の計算

        return y    出力層L2を返す

たったこれだけでニューラルネットを定義できちゃうんだから便利でいいわ．

もっと層数が多かったり多次元だったりするニューラルネットを定義したければ、

    MLP(10,10,8,6,10,10,3,1)

などと記述すればいいんだろうなぁ．なんかスゲー便利じゃね？

なお、kerasというのは、TensorFlowを便利に使えるラッパーレイヤーです．より一層black boxに....

In[4]: 誤差計算を定義する

bce = tf.keras.losses.BinaryCrossentropy()      出来合いの誤差計算objectを流用

def loss(t, y):

    return bce(t, y)

tは赤青の教師フラグで０または１

yはニューラルネット出力で０～100％

BinaryCrossentropy()は内部で何をやっているのか？

sourceを読んだわけじゃないので概ね想像ですが、、、

Binaryというワードの意味するところは、ｔ＝０または１、すなわち赤青の２値分類に対応した誤差計算であると名乗っているんじゃないかと思います．

そして、ｔとｙを材料にblack boxがやっている計算は、、、

教師データが10個あるとします．ゆえに正答ｔは10個です．Xも10個です．

それぞれに対してニューラルネット出力ｙも10個得られます．ｙは０～１のfloatです．下表では％で表しています．

ｔとｙが誤差計算関数loss(t,y)に与えられますと返り値は-0.0005979です．（実際は対数で計算してるのかもしれませんが不明です）

この-0.0005979は何者なのかが重要です．

１番目： 正答は１です．ニューラル君は75%だと言ってる．>50%なのでニューラル君も１だと判定しました．おめでとう正解です．得点は75点です．

２番目： 正答は０です．ニューラル君は27%だと言ってる．<50%なのでニューラル君も０だと判定しました．おめでとう正解です．得点は100-23=73点です．

３番目： 正答は０です．ニューラル君は「96%だから絶対１だ」と主張しました．残念ですが大ハズレです．得点はたったの100-96=４点です．

10番目まで計算すると、得点（ｔとのマッチ度）が10個出てきます．10個の得点を掛け算したものが0.0005979です．さらに符号反転して-0.0005979です．

掛け算ですから、10個とも100点だったらloss()=-1で最高得点です．３番目みたいな「大外し」をしでかすと鬼の様に足を引っ張ってloss()=0に近づいてしまいます．

ニューラルネットは教師あり学習を積み重ねることによって、lossの最小化（-1に近づける）を図ります．

In[5]: ニューラルネット内部に隠れたwとbを１回だけ修正するルーチン

optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)   修正object

def train_step(x, t):    修正ルーチン

    with tf.GradientTape() as tape:   内部状態を記録する謎のblack-box

        outputs = model(x)    ニューラルネットMLPのインスタンス

        tmp_loss = loss(t, outputs)     誤差を計算する

    grads = tape.gradient( tmp_loss, model.trainable_variables)    自動微分

    optimizer.apply_gradients(zip(grads, model.trainable_variables))    修正

    return tmp_loss     誤差を返して終了

Ｗ修正のキモはどうやって微分するの？ってことです．微分さえできてしまえば後はお茶の子さいさいですから．とするとGradientTapeが最重要ですがblack-boxでワケワカメ．

TensorFlow tutorialにGradientTapeの解説が少しあります．GradientTapeは内部計算の全てを記憶するそうです．またトップダウン型自動微分が実装されているとのこと．wikiの自動微分へリンクされていて、自動微分は数式微分でも数値微分でもないと書かれています．

自動微分とはなんぞやですが、ひら理解によると、合成関数の微分で順次解いてゆく計算手法で、ボトムアップ型自動微分は以下のような事をやっているみたいよ．

１）W111で偏微分したいとすると、ニューラルネットのW111～yまでを残して他は全部切り捨てる．そうしないと混ざってしまって偏微分にならないと思う．

２）u11=w111 x1 をw111で微分する   ②

３）sgd=sgd(u11) をu11で微分する     ③

４）u21=w211 sgd をw211で微分する    ④

５）y=sdg(u21) をu21で微分する      ⑤

６）微分＝②③④⑤

個々の微分を実行するには、各変数の⊿が必要です．⑤の場合は⊿yと⊿u21が必要です．それはたぶん、１回過去の修正動作時のyやu21との差分を採用しているのだと思います．⑤=⊿y/⊿u21と計算すれば微分できたことになるんじゃね？

wikiによるとこのような自動微分は1960年代に最初の論文が出ているらしい．便利なことを考えてくれる人がいてよかったですね．

In[6]: いわゆるmain()がここ

model = MLP(2, 1)         隠れ２次元、出力１次元のニューラルネットを生成

for ～ next

        tmp_loss = train_step(x_[start:end], t_[start:end])     train_step()はIn[5]で記述した修正ルーチン

他のごちゃごちゃした物は割愛

何をやってるかだいたい想像ついた感じー．

自動微分というものを初めて知りました．

めんどくさいニューラルネット等の記述が簡単ポンで便利でよかよか．

かしこ